El 17 de enero de 1945 ya se podía escuchar el ruido de la artillería rusa desde los barracones del Konzentrationslager Auschwitz. El propio Himmler, Reichsführer-SS, jefe de todas las policías del Tercer Reich Alemán, ordena la evacuación total. “Ningún prisionero de los campos de concentración debe caer en manos del enemigo”, decían las órdenes. Auschwitz paraliza toda su siniestra actividad.

Un criminal alemán tendrá el sórdido privilegio de ser el último prisionero en recibir un número de serie, el 202499. El 18 de enero se movilizan más de cincuenta mil prisioneros, mal nutridos y sin ropas de abrigo, y comienza la llamada marcha de la muerte: un traslado en mitad del invierno polaco, con temperaturas de dos cifras bajo cero, con largas caminatas a pie y penosos transportes en camiones o vagones de tren sin techo. Un viaje de los prisioneros a nuevos campos de concentración en el interior de Alemania del que se estima que un cuarto de ellos no llegó a sobrevivir. En esas tremendas circunstancias, de las más atroces que produjo el siglo XX, camina Jacques Feldbau, un joven matemático judío de 30 años, hablando con otro prisionero sobre el último Teorema de Fermat.
Aunque sería fácil caer en el estereotipo del matemático aislado fríamente de su entorno y absorbido por su quehacer intelectual este no es el caso de Jacques Feldbau. En julio de 1939, dos meses antes de que empezara la encarnizada guerra europea que tantas vidas habría de truncar, se había proclamado, nadando en una piscina parisina, campeón universitario francés de los 200 metros mariposa. Durante la ocupación alemana de Francia, habiendo sido expulsado de su plaza de profesor por ser judío y mientras colaboraba clandestinamente con la resistencia francesa, compaginaba sus estudios de doctorado en la Universidad de Clermont-Ferrand (donde se habían refugiado los matemáticos judíos de su universidad de origen, la de Estrasburgo) con largas rutas en bicicleta de carretera por las montañas de la zona. No tenía problema esquiando y era un buen jugador de fútbol. Tocaba el piano con soltura y, en palabras de un conocido, “gracias a su sinceridad, bondad y carácter alegre, solo tiene amigos”. A Jacques no le faltan, pues, los temas de conversación, pero si habla de matemáticas con otros prisioneros durante esa caminata y en su estancia en Auschwitz es, como reconocerían muchos supervivientes después en sus relatos, para mantener en pie la razón ante tanta barbarie. El pensamiento matemático como una expresión máxima de la racionalidad y la humanidad frente a la desmesura de los sentimientos y pasiones básicos que nutren el radicalismo político, que señala y culpabiliza a sectores de la población y que sube naciones enteras al tren de la guerra.
Jacques Feldbau no tuvo la suerte de vivir en tiempos tranquilos. Nació en Estrasburgo el 22 de octubre de 1914, cuando la región de Alsacia aún pertenecía al Imperio alemán, en una familia judía de fuertes convicciones religiosas. La región no pasó a ser francesa hasta 1919 tras el fin de Primera Guerra Mundial, por lo que primer idioma de Jacques, de los muchos que llegaría a dominar, sería siempre el alemán. A finales de los años 20 y principios de los 30, cursa estudios de secundaria en su ciudad natal y es descrito como alumno brillante aunque algo vago. Prepara el examen de acceso a la prestigiosa École Normale Supérieure pero no llega a realizar la prueba de acceso, que era un sábado, anteponiendo sus convicciones religiosas a su futuro académico, y termina accediendo a la Universidad de Estrasburgo en 1934. Allí, con Henri Cartan y André Weil entre sus profesores, cursa sus estudios de matemáticas con buenos resultados y, tras realizar una estancia de un año como alumno invitado en la École Normale Supérieure, termina superando la prueba de la Agregation (examen que permite el acceso a la enseñanza) a pesar de dejar de asistir, de nuevo, a una prueba oral por ser en sábado.

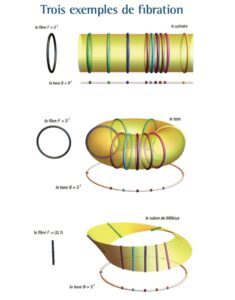
En el otoño de 1938, cuando Feldbau comienza sus estudios doctorales, iniciando así su carrera como matemático, el ambiente en su ciudad natal ya estaba muy enrarecido por las tóxicas ideas prebélicas. En la Maison Kammerzell, nombre del hermoso edificio situado a la entrada de la plaza de la catedral de Estrasburgo, un cartel de “Hunden und Juden verboten” (prohibido perros y judíos) recibía a los clientes del restaurante. El Partido alsaciano obrero y campesino difundía las ideas favorables a la Alemania nazi sin ningún rubor. Los incidentes se multiplicaban y Feldbau se vio envuelto en algunos de ellos. Pero las matemáticas eran ya su ocupación favorita y se había interesado en la topología tras asistir a un curso de André Weil, por lo que se dirigió a él buscando un tema para su tesina. Weil es considerado uno de los matemáticos más importantes del siglo XX, pero en esa época, ya sea por que era celoso de su tiempo, ya sea por la irrupción de la guerra, no parece haber dedicado mucha atención a formar estudiantes de doctorado y derivó a Feldbau hacia Charles Ehresmann que acababa de ser nombrado profesor en la Universidad de Estrasburgo. Ehresmann no tuvo problemas en dirigir la atención de Feldbau hacia cuestiones de topología algebraica y en mayo de 1939 Feldbau defendía con éxito su primera tanda de resultados, publicada en la Academia de Ciencias bajo el nombre de “Sur la classification des espaces fibrés”. Aquí estaban ya resultados de la teoría de espacios fibrados, que estaba naciendo en aquel momento, y que desde entonces forma parte de las herramientas habituales en el trabajo de la topología algebraica, la topología diferencial y la física teórica. Entre esos primeros resultados figura un teorema que se invoca recurrentemente, como una propiedad natural, en muchas demostraciones topológicas relativas a fibrados, a saber, que “un fibrado sobre una base contráctil es un fibrado trivial (Teorema de Feldbau)” y que el propio Feldbau aplicó en su primera publicación para clasificar todos los fibrados posibles sobre esferas de cualquier dimensión, otro resultado de valía. Fue un comienzo muy brillante de una carrera matemática que, pocos meses después, se vería truncada por la invasión alemana de Polonia el 1 de septiembre de 1939, fecha que marca el comienzo de la Segunda Guerra Mundial.
Feldbau fue movilizado por el ejército y asignado a la base aérea de Tours, formando parte de la escuela de oficiales de Châteauroux desde octubre de 1939, y llegó a participar en misiones aéreas de bombardeo. Como es conocido, la guerra no fue muy favorable a los franceses. El 10 de mayo de 1940 el ejército alemán cruzaba Holanda y Bélgica, esquivando todas las defensas francesas del este, y entrando en París el 14 de junio. El 22 de Junio Francia firmaba el armisticio y era dividida en dos partes: la ocupada por Alemania y la gobernada por el régimen de Vichy, colaboracionista con las ideas de la Alemania nazi. Feldbau quedó de este último lado, y al ser desmovilizado del ejército, pasó a ser profesor de la escuela de Châteauroux. Pero aunque la guerra ha terminado, la pesadilla continúa, pues el 3 de Octubre de 1940 el gobierno de Vichy comienza a promulgar su infame legislación antisemita, prohibiendo a los judíos ejercer la enseñanza.
Feldbau busca salidas y en noviembre escribe al matemático suizo Georges de Rahm mostrando interés en las ideas de la escuela suiza sobre la topología diferencial, pero termina imitando a sus profesores Ehresmann y Weil, también judío, que se habían desplazado a Clermont-Ferrand con el traslado de toda la Universidad de Estrasburgo como institución (llamada entonces Universidad de Clermont-Estrasburgo). Se instala allí en diciembre y su familia se reúne con él en abril de 1941. Aunque limitado, el ambiente de investigación matemática seguía existiendo en la universidad. El matemático Laurent Schwartz, que diez años después sería el primer francés en obtener una Medalla Field, también era judío y también estaba en ese momento allí, por lo que puede describir el ambiente de trabajo en aquella época: “Él me enseñó mucho sobre topología algebraica y llegamos a ser buenos amigos. Yo había estudiado topología algebraica en unos apuntes sobre homología escritos por Ehresmann, y Feldbau me enseñó cohomología, inventada por Kolmogorov.” Otro amigo dijo de él: “Todo era fácil para él. Hablaba varios idiomas, era un hombre de gran inteligencia y humanidad. También tenía un gran sentido del humor.”

El trabajo produce frutos y en 1941 publica, junto con su profesor Ehrenmann, “Sur les propriétés d’homotopie des espaces fibrés” donde estudia la homotopía de los fibrados a través de levantamientos de la homotopía del espacio base (ver explicación fibrados). Pero la situación se complica cada vez más para los judíos en Francia. André Weil, por ejemplo, ya ha emigrado a Estados Unidos y los que se quedan comienzan a tomar precauciones. A partir de entonces Feldbau pasa a firmar sus publicaciones bajo el seudónimo de Jacques Laboureur (traducción directa de su apellido al francés) y sus dos últimos trabajos reconocidos los firma con ese nombre. Son Les structures fibrées sur la sphère et le problème du parallélisme (1942) y Propriétés topologiques du groupe des automorphismes de la sphère (1943). De hecho, se ha planteado la posibilidad de que algunos de los trabajos publicados en esa época por Ehresmann estaban realizados conjuntamente con Feldbau, cuyo nombre habría sido eliminado durante el proceso de publicación siguiendo la consignas de unas autoridades cada vez más restrictivas con las actividades llevadas a cabo por los judíos.
Sus trabajos doctorales estaban terminados y el plan era defenderlos antes de que terminará el año, pero el 24 de junio dos agentes de la Gestapo, agencia que había ocupado la ciudad el año anterior, fueron asesinados a tiros por la resistencia y comenzó una gran redada en toda la zona. El 25 de junio, Feldbau planeaba ocultarse y pasó por la habitación de su residencia para recuperar las notas de su tesis, encontrando allí soldados alemanes y agentes de la Gestapo en pleno interrogatorio. Fue detenido y puesto en prisión en La Malcoiffée, edificio reformado de un antiguo castillo con una torre “mal terminada”, donde los alemanes encerraron a judíos y miembros de la resistencia durante la ocupación. Posteriormente fue trasladado al campo de prisioneros de Drancy, cerca de París, lugar que recibía a los judíos que iban a ser enviados a campos de concentración en Polonia. El 7 de octubre de 1943, junto con cerca de un millar de prisioneros, realizó su viaje con destino a Auschwitz en un camión de ganado. Al llegar, tres días después, la mitad de los viajeros fueron dirigidos directamente hacia las cámaras de gas, pero Feldbau resultó asignado como secretario en el módulo de cirugía de la enfermería del campo.
Durante todo el tiempo que pasó encerrado, tanto en Francia como en Polonia, Feldbau dedicó su tiempo a dar clases de matemáticas, física o astronomía a sus compañeros prisioneros y, cuando tenía suerte, hablaba de matemáticas avanzadas al coincidir con algún otro matemático. Y había otros matemáticos en Auschwitz por lo que entre ellos se proponían un problema para resolver cada día, todo con el fin de mantener ocupadas sus mentes, incapaces de procesar un destino tan bárbaro y que podía haber sido tan distinto. Laurent Schwartz, que había seguido una trayectoria académica similar a la de Feldbau, quizá por tener más suerte (su frágil salud le impidió participar activamente en el movimiento de resistencia), quizá por mostrar mayor prudencia (llegó a cambiar de identidad durante un tiempo), había conseguido esquivar el tenebroso remolino del antisemitismo de la época y sus logros matemáticos nos permiten imaginar que para Feldbau podía haber existido también una brillante carrera plena de aportaciones a las matemáticas.

Pero no fue así. A pesar de su fortaleza física, que le permitió sobrevivir a la marcha de la muerte, tras su traslado a Flossenburg, en la región alemana de Baviera, y su posterior desplazamiento al campo de concentración anexo de Ganacker, quedó tan débil que acabó falleciendo el 22 de abril de 1943, quince días antes del final de la guerra. Sus restos fueron repatriados en 1957 y yacen en la actualidad en el cementerio judío de Cronenbourg, en Estrasburgo.
Los resultados de la tesis que no llegó a defender fueron publicados póstumamente mucho más tarde, pero ya habían sido difundidos y utilizados por otros matemáticos de forma anónima. En su Historia de la Topología Algebraica y Diferencial, el matemático Jean Dieudonné los describe como “descubiertos de forma simultánea por varias personas cuya comunicación había sido interrumpida por la guerra”.
|
Para aprender más sobre el tema.
|